1535. Небоскребы

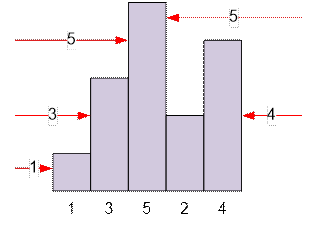
Линия горизонта в городе содержит n зданий, каждое из которых имеет уникальную высоту от 1 до n. Дом виден слева (справа), если левее (правее) его нет дома с большей высотой. Например, если дома имеют порядок {1, 3, 5, 2, 4}, то слева видны три дома с номерами 1, 3, 5, а справа два, номера которых 4 и 5.

Вам известно, что домов всего n, l домов видны слева, и r домов видны справа. Найдите количество перестановок домов, которые удовлетворяют этим ограничениям.

Вход. Каждая строка является отдельным тестом и содержит значения n (1 ≤ n ≤ 100), l и r (1 ≤ l, r ≤ n).

Выход. Для каждого теста выведите в отдельной строке количество перестановок домов, которые удовлетворяют заданным условиям. Результаты следует выводить по модулю 10⁹ + 7.

Пример входа	Пример выхода
4 2 2 5 3 2 8 3 2	6 18 4872

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

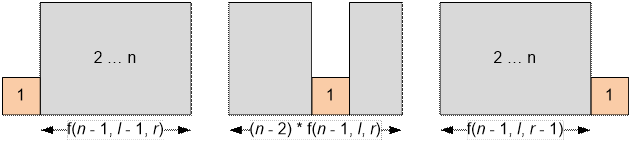
Предположим, что осталось расположить n домов, которые следует расположить так, чтобы слева было видно l, а справа r домов. Пусть это можно сделать f(n, l, r) способами. Рассмотрим дом с наименьшей высотой. Если его поставить слева, то он будет всегда видим, а оставшиеся дома можно будет расставить f(n – 1, l – 1, r) способами. Если дом с наименьшей высотой поставить справа, то он всегда будет оставаться видимым справа, остальные дома можно будет расставить f(n – 1, l, r – 1) способами. Не с краю наименьший дом можно поставить n – 2 способами. В этом случае он не будет видим, поэтому оставшиеся дома можно расставить (n – 2) * f(n – 1, l, r) способами.

Заметим, что при n = 1 единственная возможная расстановка будет лишь при l = r = 1. Получаем рекуррентное соотношение:

f(n, l, r) = f(n – 1, l – 1, r) + f(n – 1, l, r – 1) + (n – 2) * f(n – 1, l, r),

f(1, 1, 1) = 1,

f(1, x, y) = 0, когда x и y одновременно не равны 1

Пример

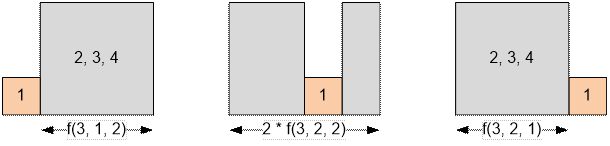
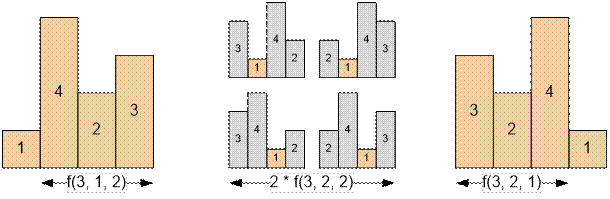
Построим все перестановки домов для n = 4, l = 2, r = 2.

f(4, 2, 2) = f(3, 1, 2) + 2 * f(3, 2, 2) + f(3, 2, 1) = 1 + 2 * 2 + 1 = 6

Реализация алгоритма

Объявим трехмерный массив dp, ячейка dp[i][j][k] которого будет сохранять значение f(i, j, k).

#define MAX 101

int dp[MAX][MAX][MAX];

Функция f возвращает количество способов, которыми можно расположить n домов, так, чтобы слева было видно l, а справа r домов.

long long f(int n, int l, int r)

{

if (n == 1) return (l == 1 && r == 1) ? 1 : 0;

if ((l < 1) || (r < 1)) return 0;

if (dp[n][l][r] != -1) return dp[n][l][r];

dp[n][l][r] = (f(n - 1, l - 1, r) + f(n - 1, l, r - 1) + (n - 2)*f(n - 1, l, r)) % 1000000007;

return dp[n][l][r];

}

Основная часть программы. Читаем входные данные. Вычисляем и выводим ответ.

while (scanf("%d %d %d", &n, &l, &r) == 3)

{

memset(dp, -1, sizeof(dp));

res = f(n, l, r);

printf("%d\n", res);

}

Java реализация

import java.util.*;

public class Main

{

static long dp[][][] = new long[101][101][101];

public static long f(int n, int l, int r)

{

if (n == 1) return (l == 1 && r == 1) ? 1 : 0;

if (l < 1 || r < 1) return 0;

if (dp[n][l][r] != -1) return dp[n][l][r];

dp[n][l][r] = (f(n - 1, l - 1, r) + f(n - 1, l, r - 1) + (n - 2)*f(n - 1, l, r)) % 1000000007;

return dp[n][l][r];

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

while (con.hasNextInt())

{

int n = con.nextInt();

int l = con.nextInt();

int r = con.nextInt();

for(int i = 0; i < 101; i++)

for(int j = 0; j < 101; j++)

for(int k = 0; k < 101; k++)

dp[i][j][k] = -1;

long res = f(n, l, r);

System.out.println(res);

}

con.close();

}

}